算法

• 基础算法：字符串、数组、正则表达式、排序、递归
• 数据结构：堆、栈、队列、链表、矩阵、二叉树
• 高级算法：贪心算法、动态规划

递归

• 定义: 在函数内部自己调用函数自己
• 死递归:没有递归结束条件
• 化归思想：化繁为简，化难为易

斐波那契数列

Fibonacci 数列: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … 求其第 n 项.

递推关系:fn(n) = fn(n-1) + fn(n - 2)

function fib( n ) {
    if ( n == 0 || n == 1 ) 
    return 1;        
    return fib( n - 1 ) + fib( n - 2 );
}

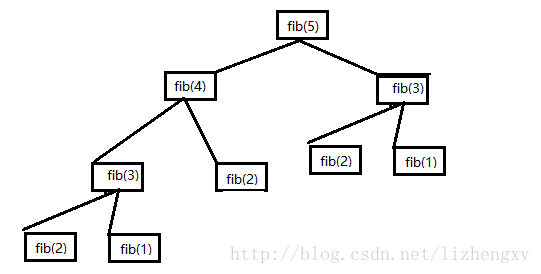
// fib(5) = fib(4) + fib(3); fib(4) = fib(3) + fib(2); 
// fib(3)重复计算，所以借助一个栈存放已经计算过的数列，如果有就直接用，没有就缓存供下次使用
// 优化：

let i = 0;
// 缓存已经计算过的数列
let temp = [];
function fib(n) {
    i++;
    if(temp[n]) {
        return temp[n]
    }else {
        if(n === 0){
            temp[n] = 1
            return 1
        }else if(n === 1){
            temp[n] = 1
            return 1
        }
        temp[n] = fib(n - 1) + fib(n - 2);
        return temp[n]
    }
}

// 也可以使用for循环
function feibo(n) {
    let temp = [1, 1]
    if(n === 1 || n == 2) {
        return 1
    }
    for(var i = 2; i < n; i++) {
        temp.push(temp[i - 1] + temp[i - 2])
    }

    return temp[n - 1]  // 长度-1
}
feibo(5)

1, 2, 3, 4, 5, ..., 100 求和

foo(100)就是求1到100的和

上面就是利用了化归思想：

• 将 求 100 转换为 求 99
• 将 求 99 转换为 求 98
• ...
• 将求 2 转换为 求 1
• 求 1 结果就是 1
• 即: foo( 1 ) 是 1

function foo(n){
    if(n === 1){
        return 1;
    }
    return foo(n-1) + n;
};
foo(100);

求 1, 3, 5, 7, 9, ... 第n项的结果与前n项和. 序号从0开始

第n项就是fn(n)

function fn(n) {
  if( n == 0 ) {
    return 1;
  }
  return fn(n - 1) + 2;
}

sum( n ) 就是前 n 项和，前 n 项和 等于 第 n 项 + 前 n-1 项的和

function sum( n ) {
  if (n == 0) {
    return 1;
  }
  return fn(n) + sum(n - 1);
}

现有数列: 1, 1, 2, 4, 7, 11, 16, … 求 第 n 项, 求前 n 项和.

求第n项

function fn( n ) {
    if( n == 0 ) 
    return 1;
    return fn(n - 1) + n - 1;
}

前n项和

function sum( n ) {
    if ( n == 0 ) 
    return 1;
    return sum(n - 1) + fn(n);
}

阶乘：一个数字的阶乘表示的是从 1 开始 累乘到这个数字. 例如 3! 表示 1_2_3. 5! 就是 1_2_3_4_5. 规定 0 没有阶乘, 阶乘从1开始。

求n的阶乘

function foo ( n ) {
    if ( n == 1 ) 
    return 1;
    return foo( n - 1 ) * n;
}

求幂

• 求幂就是求 某一个数 几次方
• 2*2 2 的 平方, 2 的 2 次方
• 求 n 的 m 次方
• 最终要得到一个函数 power( n, m )
• n 的 m 次方就是 m 个 n 相乘 即 n 乘以 (m-1) 个 n 相乘

function power ( n, m ) {
    if ( m == 1 ) 
    return n;
    return power( n, m - 1 ) * n;
}